数据结构_二叉树

前言

本文介绍了二叉树，及其应用。

树，既能像链表那样快速插入和删除，又可以像数组那样快速查找。

树

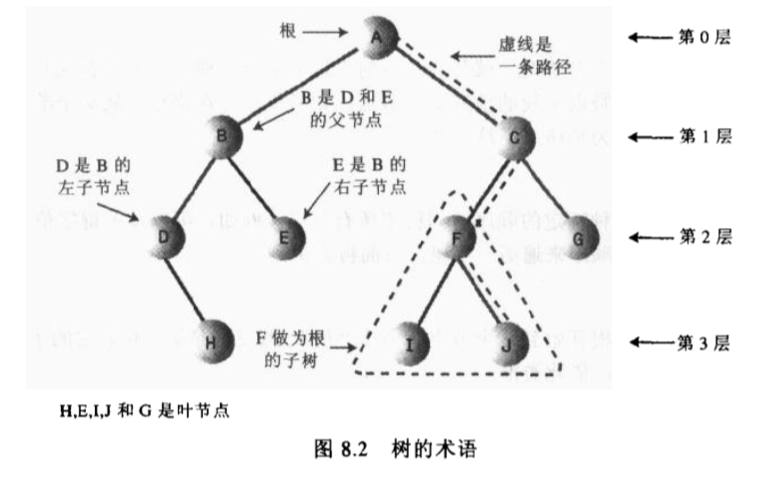
每棵树有且只有一个根，从根到任何一个节点有且只有一条路径；每个节点都可以有 0 个或者多个子节点，没有子节点的节点叫做叶子节点。

层是指从根节点到该节点的“代”树，根节点的在0 层。

二叉搜索树

一个节点只能有 0~2 个子节点的树叫做二叉树；

如果二叉树的左子节点的关键字小于该节点，右子节点的关键字大于该节点，则该二叉树称为二叉搜索树。

如下，是一个二叉树的节点：

class BinaryNode(val iId: Int, val dData: Double, var left: BinaryNode? = null, var right: BinaryNode? = null) {
    override fun toString(): String {
        return "{$iId,$dData}"
    }
}

遍历

遍历树指安装一定的顺序访问数的每个节点，按照访问节点的顺序不同，可以分为三种：

• 前序遍历
• 中序遍历
• 后序遍历

以中序遍历为例，其访问节点的顺序如下：

1. 调用自身遍历该节点的左子树；
2. 访问这个节点；
3. 调用自身遍历该节点的右子树。

实现如下：

/**
 * 中序遍历法
 * 使所有节点的关键值按照升序被访问
 */
fun inTraversing(node: BinaryNode?) {
    if (node == null) {
        return
    }
    inTraversing(node.left)
    print("$node,")
    inTraversing(node.right)
}

最大值和最小值

二叉搜索树的最大值是右子树中最右端没有子节点的右子节点；

二叉搜索树的最小值是左子树中最左端没有子节点的左子节点。

删除

二叉搜索树因为节点要满足左子节点 < 节点 < 右子节点这个条件，所以删除需要分以下几种情况：

按照要删除的节点子节点数目的不同，分为 3 种情况

• 要删除的节点是叶节点 将其父节点的指向设为 null 即可

• 要删除的节点有且只有一个节点 将其父节点指向其子节点

• 要删除的节点有两个子节点 这时候可以找该子节点的右子树中最小的（或者左子树中最大的）节点并替换掉要删除的节点，

  与此同时如果这个节点有右子节点（或对应的左子节点）则按照 2/3 的规则处理，这样就能保证这个树的结构不会出错

fun delete(iId: Int) {
        //查找 iId 对应的节点
        var current = root
        var parent = root
        while (current?.iId != iId) {
            if (current == null) {
                return
            }
            parent = current
            current = if (iId > current.iId) {
                current.right
            } else {
                current.left
            }
        }
        if (parent == null) {
            return
        }

        /**
         * 按照要删除的节点子节点数目的不同，分为 3 种情况
         * 1/3 要删除的节点是叶节点 将其父节点的指向设为 null 即可
         * 2/3 要删除的节点有且只有一个节点 将其父节点指向其子节点
         * 3/3 要删除的节点有两个子节点 这时候可以找该子节点的右子树中最小的（或者左子树中最大的）节点并替换掉要删除的节点，
         *     与此同时如果这个节点有右子节点（或对应的左子节点）则按照 2/3 的规则处理，这样就能保证这个树的结构不会出错
         *     下面采用的是找该节点的右子树最小值，即右子节点或者右子节点的最后一个左子节点
         *     找到后用该子节点的值替换掉要删除的节点值，如果该子节点还有右子节点，将该子节点的父节点指向其右子节点
         */
        if (current.left != null && current.right != null) {
            //双子节点

            // 当前点右子节点的左子节点为 null
            if (current.right!!.left == null) {
                if (current.iId > parent.iId) {
                    parent.right = current.right
                } else {
                    parent.left = current.right
                }
                //TODO 是否需要将右节点的左子节点指向当前点的左子节点
                return
            }

            var cChildNode = current.right
            var cParentNode = current!!

            while (cChildNode?.left != null) {
                cParentNode = cChildNode
                cChildNode = cChildNode.left
            }

            //后继节点
            cParentNode.left = cChildNode!!.right
            cChildNode!!.right = current.right
            cChildNode!!.left = current.left
            if (current.iId > parent.iId) {
                parent.right = cChildNode
            } else {
                parent.left = cChildNode
            }

        } else if (current.left == null && current.right == null) {
            //叶子节点
            if (current.iId > parent.iId) {
                parent.right = null
            } else {
                parent.left = null
            }
        } else if (current.left == null) {
            if (current.iId > parent.iId) {
                parent.right = current.right
            } else {
                parent.left = current.right
            }
        } else if (current.right == null) {
            if (current.iId > parent.iId) {
                parent.right = current.left
            } else {
                parent.left = current.left
            }
        }

    }

哈夫曼编码

哈夫曼编码用来对一段文本进行压缩，解压。

压缩：用字符的编码替代字符

解压：用字符代替对应的编码

实现思路如下：

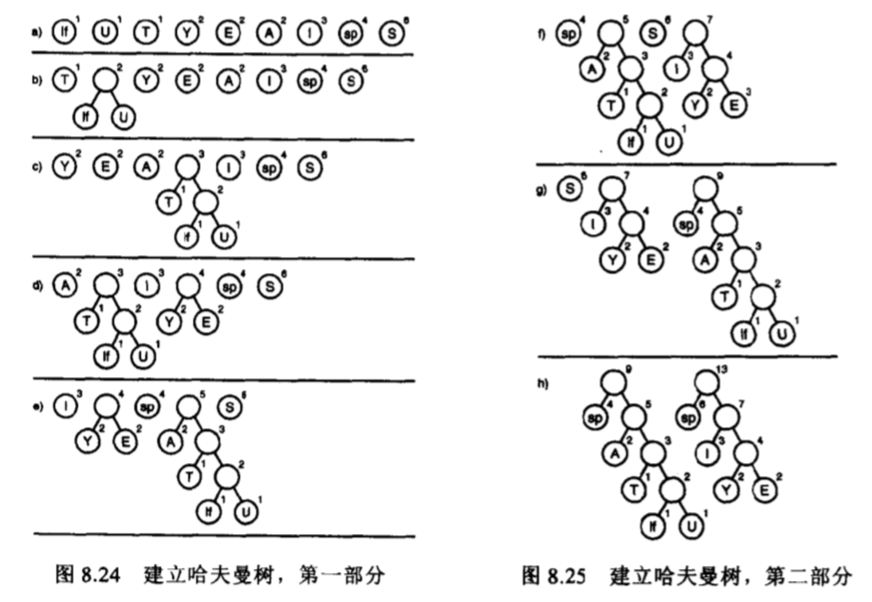
•          将字符按照出现的频次生成优先级队列；
  

•          依次**取出**两个最小的字符，为他们生成一个父节点（父节点频次为两个子节点之和）；
  

•          并将插入优先级队列中，依次循环直到优先级队列中只有一个节点——哈夫曼树的根节点；
  

•          从哈夫曼树的根开始，以向左为 0，向右为 1 对其叶子节点上的字符赋予编码。
  

其过程如下图所示：

哈夫曼编码示意图

源码

👉 点这里 查看二叉树源码

👉 点这里 查看哈夫曼编码源码