数据结构_高级排序

前言

本文介绍两种高级排序：希尔排序和快速排序。

希尔排序的时间复杂度是$O(N*(LogN)^2)$，简单易实现，在所有排序中可以优先使用。

快速排序的时间复杂度是$O(N*LogN)$，是所有通用排序中最快的。

排序方向：小 → 大。

希尔排序

希尔排序基于插入排序（将左边无须的元素依次插入到右边有序数组中），不同的是希尔排序的增量逐渐减小到 1，而插入排序的增量一直是 1。

增量 排序的时候进行比较的两个元素之间的间隔：

int[] arr = {1,2,3,4,5};

对于数组arr中的元素来说，1和 2之间的增量是 1，而 1和 3之间的增量是 2，以此类推。

由于插入排序在排序进行到后期，右边有序数组的大小变大，导致插入和移动的次数越来越多，而且如果数组恰好是反序的，会很耗时。

而希尔排序在刚开始排序时，先取一个适当的增量n，按照这个增量对数组arr进行插入排序，得到一个基本有序的数组，他内部有n个有序的子数组；再将增量n减一，在此进行插入排序；如此反复直到 n 为 1，排序完毕的数据即为有序数组。

希尔排序——4 增量排序示意图

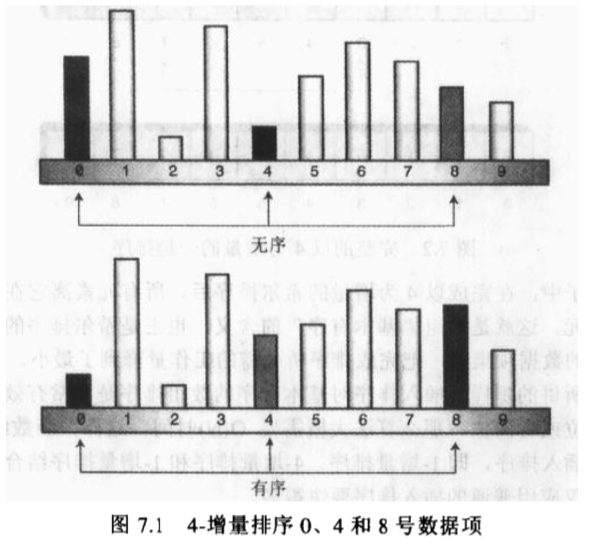
增量的选择

可以想象，增量的计算对希尔排序效率有很大影响。

这些增量的集合称为间隔序列，一般要求这些增量之间互质，这样就不会对已经排序的数组再次排序。

一个常用的间隔序列计算公式：

h=3h+1
计算的h值一般为：1,13,40,21...

增量h要小于数组大小。

具体实现

/**
 * 希尔排序
 * 思路：
 * 1/3 将待排序数组分为 h 个间隔为 h 的小数组，
 * 2/3 对这些小数组进行插入排序，将排序结果写入原待排序数组
 * 3/3 按照 h=3*h+1 的算法减小 h 在此进行希尔排序，直至 h 为 1
 * --将大数组分为较小的数组，拍完序后再对这些"有序"的小数组进行排序
 * 小 - > 大
 */
fun shellSort(intArray: IntArray, h: Int): IntArray {
    if (h == 1) {
        return insertSort(intArray)
    } else {
        //间隔排序
        for (x in 0 until h) {//依次遍历 x,x+1,x+2 ... x+(h-1);形成 h 个有序子数组

            var list = arrayListOf<Int>()
            intArray.forEachIndexed { index, i ->
                if ((index + x) % h == 0) {
                    list.add(i)
                }
            }
            var partSortArr = insertSort(list.toIntArray())
            var listIndex = 0
            intArray.forEachIndexed { index, i ->
                if ((index + x) % h == 0) {
                    intArray[index] = partSortArr[listIndex++]
                }
            }
        }

        //将增量减小，再次减小排序，直到 h==1
        return shellSort(intArray, (h - 1) / 3)
    }
}

/**
 * 获取希尔排序间隔
 * 对排序速度影响较大，要求互质，计算方式不唯一
 */
fun getShellSortH(range: Int): Int {
    if (range < 5) {
        return 1
    }
    var h = 1
    while (h < range) {
        h = 3 * h + 1
    }
    return (h - 1) / 3
}


/**
 * 插入排序
 * 思路：
 * 1/2 先假设第一个数是已经排好序的
 * 2/2 将后面的数字依次与其比较，并插入到对应位置
 * small -> big
 */
fun insertSort(intArray: IntArray): IntArray {

    for (i in 1 until intArray.size) {
        for (j in 0 until i) {
            if (intArray[i] < intArray[j]) {
                val temp = intArray[i]
                for (x in i downTo j) {
                    if (x - 1 < 0) {
                        break
                    }
                    intArray[x] = intArray[x - 1]
                }
                intArray[j] = temp
            }
        }
    }

    return intArray
}

快速排序

快速排序在大多数情况下都是最快的。

划分

划分指在一组数据中，指定一个值C,所有小于C的移动到左边，所有大于C的移动到右边。

选出来的这个值C，叫做枢纽。

划分算法

• 在数据左右两端各有一个指针指向当前元素：left，right；
• left指针向右移动查找比C大的值，right指针向左移动查找比C小的值，当遇到满足条件的元素则退出；
• 当两个指针都退出时，将其指向的元素交换位置，然后再分别移动指针，直到两个指针相遇，划分结束。

快速排序的思路

快速排序，选取一个枢纽，将数组划分为两个子数组，这样在枢纽C两边的数组满足：

[左边子数组所有元素] < n < [右边子数组所有元素]

这样将得到的每个子数组都划分为两个子数组，直到子数组只有一个元素（一个元素就是有序的），这样就完成了整个快速排序。

枢纽的选择

枢纽选择影响着快速排序的效率：

• 最简单的，可以选取数组第一个或者最后一个元素
• "三数据项取中"法，在数组首、尾、中取数排序，选中间的数作为枢纽。这样排序数组大小要>3。

具体实现

/**
 * 快速排序所用的数组，使用前先初始化
 */
lateinit var quickArray: IntArray

/**
 * 快速排序算法
 * #1 选择数组最右端元素作为枢纽
 * 思想是
 * 1/2 选出一个枢纽，先将其按大小划分为左右两部分
 * 2/2 在划分好的两个数组中，分别再找一个枢纽，重复步骤 1
 */
fun quickSort1(left: Int, right: Int) {
    if (right - left <= 0) {
        return
    }
    /**
     * n 这个枢纽的取法很关键，决定了算法的速度
     * 除过这里用到的取法之外，还可以有"三数据项取中"法，在数组首、尾、中取数排序，选中间的数作为枢纽。这样排序数组要>3
     * 对于这些小于 3 的数组可以用插入排序法进行排序
     */
    val n = quickArray[right]
    val nIndex = devideArrayByN1(left, right, n)
    if (nIndex > 0) {
        quickSort1(left, nIndex - 1)
    }
    quickSort1(nIndex + 1, right)
}

/**
 * 划分算法决定了排序的准确性
 * 提出一个阈值，并以此将数组划分为两部分
 * 左边都小于枢纽，右边都大于枢纽
 */
private fun devideArrayByN1(left: Int, right: Int, n: Int): Int {
    var leftIndex = left - 1
    var rightIndex = right

    while (leftIndex < rightIndex) {
        while (leftIndex < rightIndex && quickArray[++leftIndex] < n) {
        }
        while (leftIndex < rightIndex && quickArray[--rightIndex] > n) {
        }
        val temp = quickArray[leftIndex]
        quickArray[leftIndex] = quickArray[rightIndex]
        quickArray[rightIndex] = temp
    }

    for (i in right downTo rightIndex) {
        if (i < 1) {
            break
        }
        quickArray[i] = quickArray[i - 1]
    }
    quickArray[rightIndex] = n
    return rightIndex
}

总结

希尔排序、快速排序的思路，都是将一个大的待排序数组，通过不同的方法拆分成小的子数组，这样比较、移动的次数要小很多。

源码

👉 点这里 查看源码