前言
堆是一种特殊的二叉树,用他实现的优先级队列插入和删除时间复杂度都是$O(LogN)$ 。
特征
- 堆是完全二叉树*
- 常用数组实现
- 每个堆的节点都满足堆的条件,即堆的每个节点关键字都大于(或等于)子节点的关键字
特征3保证了根节点是堆中最大的值,以及顺着某一个节点一直到遇到叶节点的路径上的节点关键字是依次递减的,但是没法保证这个值是这个堆中的最小值,这是因为堆中每个节点的左右子节点的位置和大小无关,两条这样的路径之前的值的大小没有一定的关系。
操作
堆可以进行插入、移除,遍历等操作,时间复杂度都是$O(LogN)$。初次之外,利用堆根节点关键值最大这个属性,还可以进行堆排序,时间复杂度为$O(N*LogN)$。
对于在数组中保存的堆,设元素下标为x,则各个相关元素下标如下:
- 父节点
(x-1)/2 - 左子节点
2*x+1 - 右子节点
2*x+2
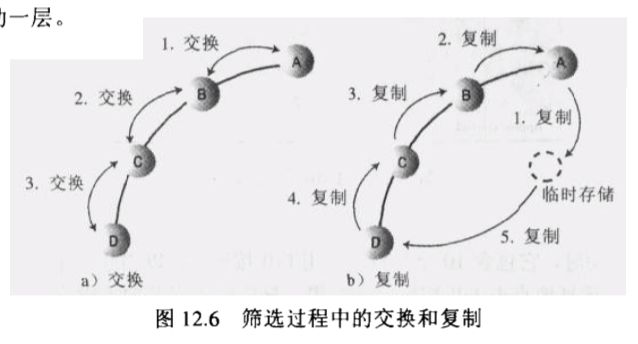
在插入,移除的时候为了保证满足堆的条件,需要对堆进行向上或向下的遍历,将修改的值移动到对应的位置,在这过程中涉及到复制和交换。如果每次比较都需要交换数据的话会复制很多次,而如果将最终要移动值保存在临时变量中,用一个值专门记录要移动到的下标,在每次符合条件时只复制参与对比的值,在最后再将要临时保存的值复制到目的下标,就会减少复制的次数。
如下图就将复制次数从 9 次减少到了 5 次。
插入
插入操作思路是,将元素插入到数组最后一位,然后依次向元素父节点遍历,将不满足的元素下沉,直到找到满足堆特征3(父节点关键字大于该点,并且子节点关键字小于该点)的下标,或者指向了根目录,将该元素插入该处。
/**
* 从下向上遍历
* 如果父节点比插入值小,就将父节点移动到插入值的位置,将toIndex指向空出的地方
* 依次查找,直到查找到父节点比插入值大,子节点比插入值小的地方,或者指向了根节点
*/
private fun checkUp(index: Int) {
var bottom = headArray[index]//headArray是保存堆元素的数组
var toIndex = index
var father = (toIndex - 1) / 2
while (toIndex > 0 && bottom!!.key > headArray[father]!!.key) {
headArray[toIndex] = headArray[father]//将父节点下沉
toIndex = father
father = (toIndex - 1) / 2
}
headArray[toIndex] = bottom//将该值插入到对应下标
}
移除
移除指的是将根节点推出堆中。
基本思路是将根节点推出,再将数组最后一个节点(同时也是堆的最后一个节点)移动到根节点空出的位置,再依次向下遍历,直到将该节点放到符合堆条件的位置或者到达叶子节点。
和插入相比,移除时要移动的节点要比较的稍微多些。
- 该节点是叶节点 直接插入 ✅
- 有两个子节点 和两个叶子节点中最大的比较,如果小于则交换,并再和新的子节点比较
- 只有左节点 如果左节点大于本节点则交换,否则就是该位置
/**
* 从上向下遍历
* 如果遇到比当前值top大的就将其复制到当前位置toIndex,并记录下空出的位置为toIndex
* 再以toIndex为起点向下比较,直到遇到top比父节点小,比子节点大的位置,或者叶子节点
* 将top移动到该位置
*/
private fun checkDown(index: Int) {
var toIndex = index
var top = headArray[size - 1]!!
while (toIndex < size / 2) {//非叶子节点
var leftIndex = 2 * toIndex + 1
var rightIndex = 2 * toIndex + 2
if (headArray[rightIndex] == null) {//只有左节点
if (headArray[leftIndex]!!.key > top.key) {
headArray[toIndex] = headArray[leftIndex]
toIndex = leftIndex
} else {
break
}
} else if (headArray[leftIndex] != null && headArray[rightIndex] != null) {
if (headArray[leftIndex]!!.key >= headArray[rightIndex]!!.key) {//如果左节点比较大
if (headArray[leftIndex]!!.key > top.key) {
headArray[toIndex] = headArray[leftIndex]
toIndex = leftIndex
} else {
break
}
} else {//如果右节点比较大
if (headArray[rightIndex]!!.key > top.key) {
headArray[toIndex] = headArray[rightIndex]
toIndex = rightIndex
} else {
break
}
}
}
}
headArray[toIndex] = top//将该节点移动到找到的下标处
}
堆排序
利用堆根节点关键值最大这一特性,可以进行堆排序。
只需要将待排序的数组依次插入堆中,然后再依次移除即可。
这样需要有两倍与待排序数组大小的空间。如果每次插入时候只保存数据,不进行向上遍历,在每次移除数据时进行向下遍历,将当前剩余数据最大值选出来(其余数据仍然无序)从堆中移除根元素时都会在数组末尾空出一个位置,将该值存储在该位置即可,这样等完全插入、移除后就得到一个有序数组【从数组末尾开始依次减小】
堆排序和快速排序时间复杂度都是 O(N*LogN) ,但是由于向上、向下遍历耗时,实际上要比快速排序稍慢一些。但是堆排序堆数据初始分布不敏感一直都是 O(N*LogN) ,快速排序在某些情况下时间复杂度可达到 O(N^2) 。
附录
满二叉树
满二叉树指除最后一层无任何子节点外,每一层上的所有结点都有两个子结点二叉树。
如果一个二叉树的层数为 K,且节点总数是 $(2^k) -1$ ,则它就是满二叉树。
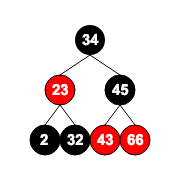
完全二叉树
完全二叉树 如果将二叉树每层从左到右遍历,那么完全二叉树只有最后一层的右边会出现没有叶子节点的情况,即在前 1~n 之间没有“洞”。
如下图就是一个完全二叉树:
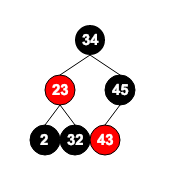
但下图不是完全二叉树:
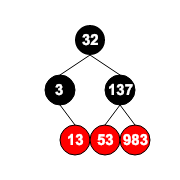
源码
👉 点这里 查看源码
参考链接
《Java 数据结构和算法 (第二版)》 Robert Lafore 陈维宁
有想法?欢迎通过邮件讨论。