数据结构_图

JI,XIAOYONG原创...大约 6 分钟

前言

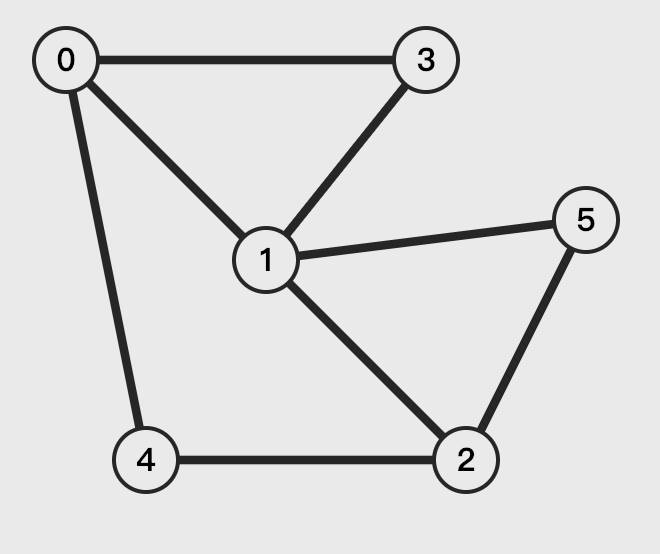
图，是由可以有多个边的顶点组成的结构。

两个顶点之间有边连接，则称这两个顶点是邻接的。

几个相互邻接的顶点组成的线叫做路径,至少有一条路径可以到达所有顶点的图叫做连通图。

如果图的顶点只能从 A→B，不能从 B→A，就称图是有向图。

如果边被赋予一定的权值（数字），就称图为带权图

存储方式

图一般有两种存储方式：

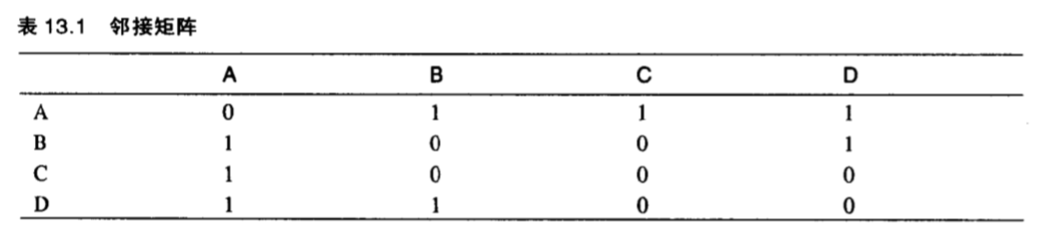
邻接矩阵用 N*N 的数组保存图中所有的顶点，Arr[m][n]即表示 m、n 顶点是否邻接（Y:1,N:0）。
比较占地方。
邻接矩阵
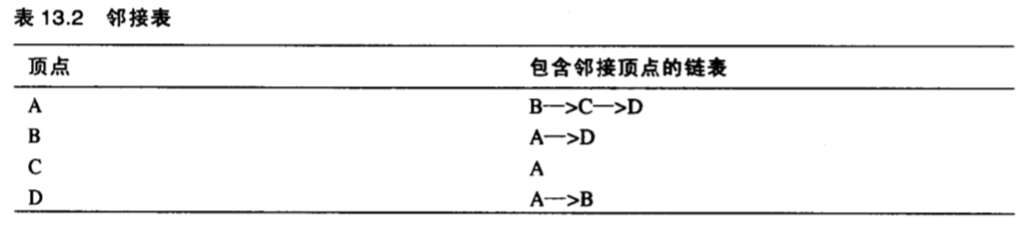
邻接表用一个 N 大小的数组保存，数组元素是保存着顶点和他所有的邻接点的链表。
邻接表

操作

图的操作有插入（顶点），搜索等等。

以下操作以邻接表方式为例。

插入

插入分为插入顶点和插入边。

插入边的时候需要注意，要同时更新 start 和 end 两个顶点对应的链表。

移除

原理同插入边。

搜索

搜索要求从某个特定顶点开始，沿着边移动到其他顶点，移动完毕后要保证访问了每个顶点。

搜索又分为 DFS（深度优先搜索）、BFS（广度优先搜索）。

DFS

DFS 的思想是，依次沿着顶点某一个邻接点，纵深访问，将该邻接点当做新的顶点压入栈中，继续纵深访问，直到有顶点没有可以访问的邻接顶点，将其打印出来（从栈中推出）；然后再返回上一层的邻接顶点中还可以访问的顶点（查找当前栈顶元素未访问的邻接点），直到没有可以访问的顶点。

用栈实现，会先往深处遍历完一条路径，再遍历下一条。每个顶点只访问一次

规则：

 1/3 访问一个邻接的未访问顶点，访问并标记，将其压入栈中；

 2/3 当规则 1 不能满足时，如果栈不为空，从栈中弹出一个顶点；

 3/3 1,2 都无法满足时，搜索结束。

private fun dfs() {
    var stacks = DfsStacks(hashMap.size)
    var keyArr = hashMap.keys.toIntArray()
    stacks.push(keyArr[0])
    hashMap[keyArr[0]]?.isVisited = true
    var index = hashMap[keyArr[0]]
    while (stacks.size > 0) {
        var availableKey = getAvailableNode(index!!.data)
        if (availableKey != -1) {
            index = hashMap[availableKey]//深度优先搜索，会先顺着一个邻接点一直走到头
            index!!.isVisited = true
            stacks.push(availableKey)
        } else {
            var pop = stacks.pop()
            print("$pop ")
            index = hashMap[stacks.peek()]//如果一个邻接点再没有未访问的邻接点，那么去访问下一个未访问的邻接点
        }
    }
}

BFS

BFS 的思想是，向将当前顶点的所有可以访问的邻接点访问完毕；之后将该顶点打印（推出），再去访问其邻接点的所有可以访问邻接点（从队列头取出一个顶点，查找其未访问的邻接点）。

用队列实现，会先遍历完本层所有的顶点，然后再移向下一层

规则：

 1/3 先访问当前顶点的所有邻接顶点，标记，并插入到队列；

 2/3 如果没有可以访问的邻接点，且队列不为空，从队列头取出一个顶点[此处又用到了一次该点]，使其成为当前顶点，重复 1；

 3/3 如果 2 不能满足，搜索结束。

private fun bfs() {
    var queue = BfsQueue()
    var keyArr = hashMap.keys.toIntArray()
    queue.push(keyArr[0])
    hashMap[keyArr[0]]!!.isVisited = true
    var index = hashMap[keyArr[0]]
    while (queue.size > 0) {
        var availableKey = getAvailableNode(index!!.data)
        if (availableKey != -1) {
            var current = hashMap[availableKey]!!//广度优先搜索，优先将一个节点的所有邻接点依次访问
            current.isVisited = true
            queue.push(current.data)
        } else {
            var pop = queue.pop()
            print("$pop ")
            if (queue.peek() == -1) {
                break
            }
            index = hashMap[queue.peek()]//如果该点没有未访问的邻接点，就选择去访问该点邻接点的邻接点
        }
    }
}

最小生成树 MST

生成树（Template:Lang-en-short）是具有图 G 的全部顶点，但边数最少的连通子图。
——维基百科

带权图的生成树中，总权重最小的称为最小生成树。

最小生成树边比顶点数小 1。

当图的每一条边的权值都相同时，该图的所有生成树都是最小生成树。
如果图的每一条边的权值都互不相同，那么最小生成树将只有一个。

无向不带权图中，只需要找出最小数量的边即可。用 DFS 比较好实现，因为他对每个顶点只访问一次。

拓扑排序

拓扑排序是指有向图的顶点排序，满足以下条件*：

每个顶点出现且只出现一次；
若 A 在序列中排在 B 的前面，则在图中不存在从 B 到 A 的路径。

实现思路是：

依次推出有向图中没有后继点的顶点作为排序的最后项，这是因为按照拓扑排序条件2没有后继点的顶点必然排在后面；
当去掉没有后继点的顶点后又会产生新的没有后继点的顶点，这样依次循环，当图中没有顶点的时候，就可以在有向无环图中完成拓扑排序。

对于有环存在（即存在类似 A→B，B→C，C→A 的情况）的有向图，会出现找不到没有后继点的顶点，但同时图中顶点数不为0的情况，遇到这种情况退出循环，并说明有环存在即可。

/**
 * 拓扑排序
 */
fun topologicalSort() {
    if (hashMap.size == 0) {
        return
    }
    var displayList = ArrayList<T?>()

    while (hashMap.size > 0) {
        var successorKey = getSuccessorNode()
        if (successorKey == null) {//图中还有顶点，但却找不到“没有后继点的顶点”，说明有环
            println("图中有环")
            break
        } else {
            hashMap.remove(successorKey)//如果找到满足条件的顶点，从图中删除并保存的排序结果中
            displayList.add(successorKey)
        }
    }
    print("\n ${displayList.reversed()} \n")//以正确的顺序输出排序结果
}

/**
 * 遍历图，查找没有后继点的顶点
 * @return -1 表示没有这样的点 否则返回该点 key
 */
fun getSuccessorNode(): T? {
    val result: T? = null
    var ketSet = hashMap.keys

    ketSet.map {//遍历图中每个顶点
        //如果顶点没有后继点 (没有邻接点，或者邻接点已经被删除) 就是满足条件
        var node: GraphicNode<T>? = hashMap[it]?.next ?: return it
        while (node != null) {
            var realNode = hashMap[node.data]
            if (realNode != null) {
                return@map//有后继点，不满足条件，查找下一个顶点
            }
            node = node.next//还有其他邻接点，依次遍历
        }
        return it
    }

    return result//没有找到“没有后继点的顶点”
}