数据结构_红黑树

前言

红黑树是一种特殊的二叉搜索树，查找，插入和删除的时间复杂度均为$O(log_2N)$。

红黑树必须满足以下条件：

1. 必须有颜色（黑/红）

2. 根节点颜色为黑

3. 若节点是红色，则子节点必须是黑色（反之则不然）

4. 到叶节点或空子节点的每一条边上的黑色节点数量必须相同（空子节点指本应该有叶节点却没有的节点，默认为黑色）

如果不满足可以通过以下方式修正：

• 改变节点颜色
• 旋转（左、右）

旋转

以某个支点旋转（右旋为例，旋转时注意更新各个节点的父节点）：

本质是将该节点a向下进一位插入到其右节点b原先的位置，将其左节点c向上进一位插入到该节点a原先的位置，并将左节点c的右节点赋值给该节点a。

步骤：

1. 将该节点a放到右节点b的位置，将该``左节点 c放到节点 a`原先的位置，依次类推

2. 特殊的，将该点a的内侧孙子（a的左子节点c的右子节点d）断开与其父节点c的连接，转而连接到a上，成为a的左子节点

如图，依次插入6,34,23，以34为支点右旋：

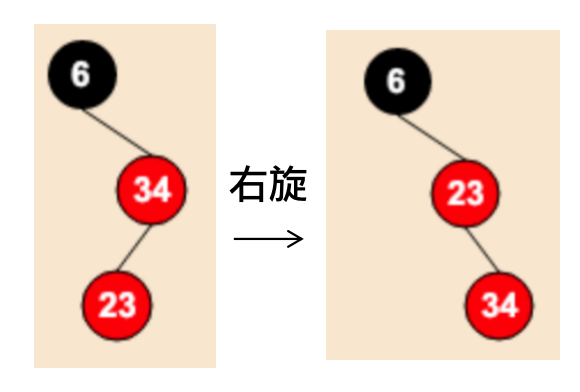
对获得的结果，由于，都是红色违反了规则3，将34的父节点23设置黑，祖父节点6设为红，以祖父节6点为支点左旋：

最终结果

插入

每次插入红色节点，能够避免规则 4。

一般先以二叉搜索树的规则将数据插入表中，然后再对照规则检查是否需要调整红黑树。

红黑树插入情况分类如下：

1. 插入位置为根节点，将节点颜色更改为黑色
2. 插入位置的父节点为根节点或父节点颜色为黑色，直接插入
3. 父节点为红色。

只有父节点为红色这种情况需要进行修正，这时又可以细分为以下三种情况：

表格来自 http://www.cnblogs.com/skywang12345/p/3245399.html#a1

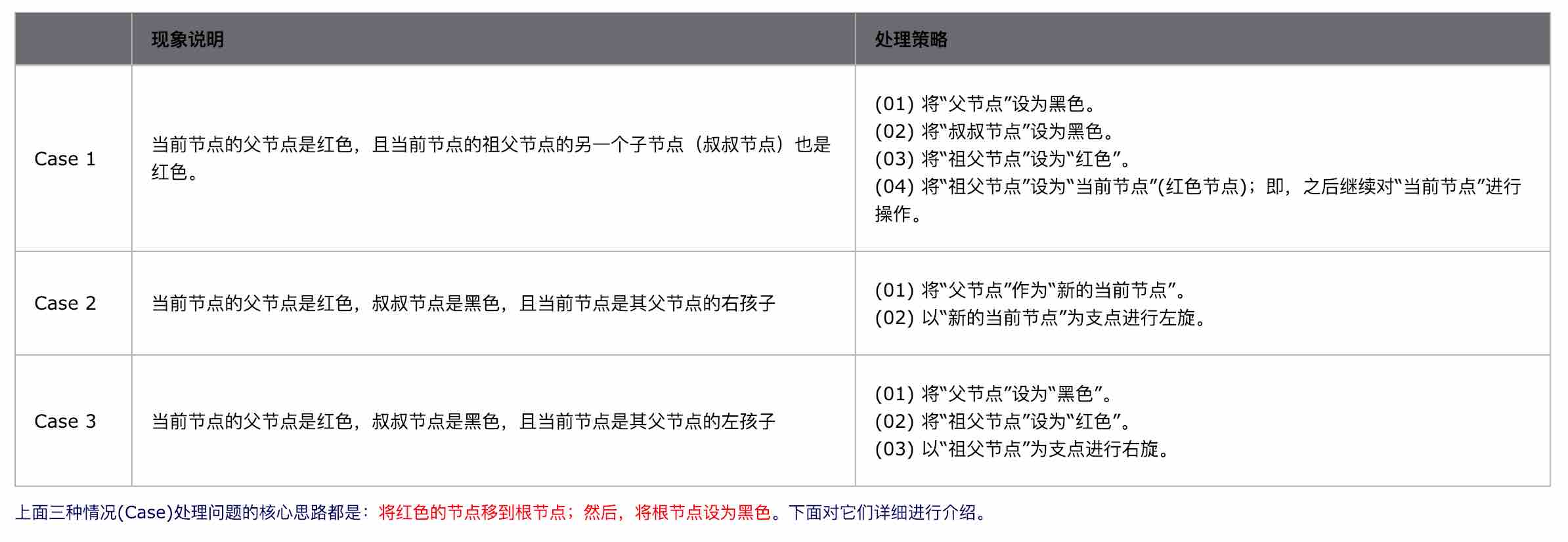
【注意】对于Case 3当祖父节点没有左节点无法右旋时的特殊处理：

需要对先对当前节点的父节点进行右旋，再以父节点作为新插入的点 N，将 N 的父节点设置为黑色，祖父节点设置为红色，以祖父节点为支点左旋。

如依次插入如下值：

32,3,53,13,983,[137],237,83,483,43,183

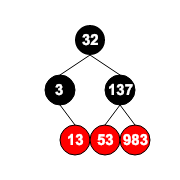
当插入137后红黑树如图：

插入 137 后的树

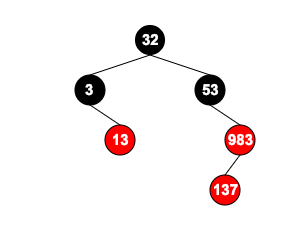
本来按照Case 3 父红 叔黑 是左节点 应该要以祖节点右旋，但是组节点 53 没有左子节点，无法右旋，所以先对父节点 983 进行右旋：

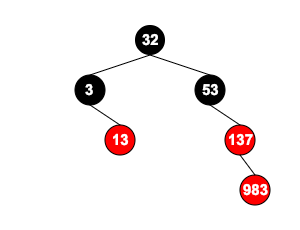
再以983为新节点，父红 叔黑 是右节点，将父节点137设置为黑色，祖节点53设置为红色，以组节点53为支点左旋：

删除

删除比较复杂，可以有两种操作：

1. 在节点中保存一个标志位，标记该节点是否被删除，并不针真的删除该点。
2. 在执行删除操作时真正删除该点。

源码

👉 点这里查看源码

参考文档

在线操作红黑树

红黑树 (一) 之 原理和算法详细介绍