数据结构_递归和汉诺塔问题

JI,XIAOYONG...大约 5 分钟

前言

本文介绍了递归，归并排序，还有递归在汉诺塔问题上的应用。

排序顺序为 小 → 大

递归

递归是一种在函数内部调用自己的函数。在满足一定条件后可以退出递归。

比如三角数组就是一个简单的递归：

有一组数据，满足这样的条件第n项 = 第n-1项 + n，就称为三角数组，如：
1,2,6,10,15,21...

这里面，第n项 = 第n-1项 + n,就是一个递归，每一项的计算结构都依赖于前一项的计算，直到第 1 项的计算结果为确定的 1，不再继续递归。

实现如下：

/**
 * 三角数
 * 第 n 个数 == 第 n-1 个数 + n
 */
fun triangleNum(num: Int): Int {
    if (num == 1) {
        return num
    }
    return num + triangleNum(num - 1)
}

汉诺塔问题

汉诺塔是一种游戏，有三个柱子，其中一棵柱子上面有若干个半径依次递减的空心圆盘，每次只能移动最顶端的圆盘，并且下面的圆盘要比上面的圆盘直径大。游戏的目的就是在满足这些条件的前提下，将所有圆盘依次转移到另外一个圆盘上面。

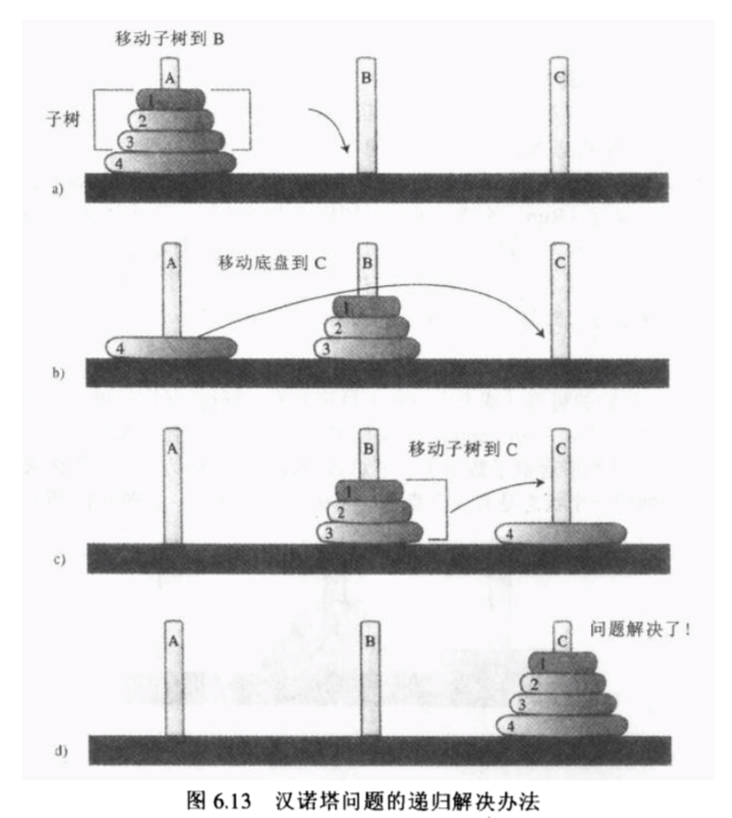
如图，实现的思路就是递归：

将除最底部的圆盘bottom之外的所有圆盘当做一个整体other，那么问题就变成了如何将bottom和other这“两”个圆盘通过柱子B，移动到柱子C，这个问题显然很好解决，只需要将other移动到柱子B，再将bottom移动到柱子C即可。
那么剩下的问题就成了如何将other从柱子A移动到柱子B，很显然可以参照步骤1。
这样子这个问题就成了如何将一个bottom从一个柱子，移动到另外一个柱子的问题，而每个这样的问题的解决都依赖于other的解决，而这就是递归。

具体实现：

/**
 * 汉诺塔问题
 * 将汉诺塔问题简化为 3 步：
 * 1/3 将最上层 n-1 项移动到过渡层
 * 2/3 将最底层 n 移动到目标层
 * 3/3 将 n-1 项移动到目标层
 * @param num 要移动的层数
 * @param from 所在层
 * @param inter 过渡层
 * @param to 目标层
 */
var hanioStepNum = 0

fun hanioTower(num: Int, from: String, inter: String, to: String) {
    if (num == 1) {
        println("move 1 to $to")
        hanioStepNum++
    } else {
        hanioTower(num - 1, from, to, inter)//把`other`移动到中间柱子
        println("move $num to $to")//把`bottom`移动到目标柱子
        hanioStepNum++
        hanioTower(num - 1, inter, from, to)//把`other`移动到目标柱子
    }
}

归并排序

归并排序merge，将一个数组，分成两个子数组分别排序，之后再将拍好序的数组合并，这样就得到了一个有序数组。时间复杂度是 $O(N*Log(N))$ 。

其思路是，将数组无限的分成两份分别进行排序，然后再将排好序的两个数组归并在一起得到有序数组。每个子数组的有序都依赖于其子数组的有序，直到每个子数组只有一个元素，这样的数组本身就是有序的。

原理如下（假设序列共有 n 个元素）：

将序列每相邻两个数字进行归并操作，形成两个n/2序列，排序后每个序列包含 1/2 元素
若此时序列数不是 1 个，则将上述序列再次归并，分别形成两个n/4序列，每个序列包含 1/4 个元素
重复步骤 2，直到所有元素排序完毕，即序列数为 1

合并两个有序的数组 (a,b) 思想：

将b中比a中小的元素都复制到a中对应位置，然后将剩下的元素全部依次复制到a的末尾。

归并排序具体实现：

/**
 * 归并排序
 * 归并排序占空间（多占一个排序数组的大小），排序快（N*LogN）
 * 思想是：
 * 1/2 将数组无限分成两份，直到两份数组都是有序的（每个数组只有一个元素）
 * 2/2 再对其进行归并
 * 小 -> 大
 * @param intArr 待排序的数组
 */
fun mergeSort(intArr: IntArray): IntArray {
    var size = intArr.size
    if (size == 1) {
        return intArr
    } else {
        var half = 0
        if (size % 2 == 0) {
            half = size / 2
        } else {
            half = (size + 1) / 2
        }
        var arr1 = intArr.copyOfRange(0, half)
        val arr2 = intArr.copyOfRange(half, intArr.size)
        return merge(mergeSort(arr1), mergeSort(arr2))//将合并好的两个有序子数组合并
    }
}

/**
 * 归并
 * 合并两个有序的数组为新的有序数组
 * 思想：
 * 1/2 相互比较两个数组每项大小，并将小的复制到新数组
 * 2/2 将剩余的数组全部复制到新数组
 * 小 -> 大
 * @param intArrA 有序数组 1
 * @param intArrB 有序数组 2
 */
fun merge(intArrA: IntArray, intArrB: IntArray): IntArray {
    var resultArr = IntArray(intArrA.size + intArrB.size)

    var indexA = 0
    var indexB = 0
    var indexC = 0

    while (indexA < intArrA.size && indexB < intArrB.size) {
        if (intArrA[indexA] < intArrB[indexB]) {
            resultArr[indexC++] = intArrA[indexA++]
        } else {
            resultArr[indexC++] = intArrB[indexB++]
        }
    }

    while (indexA < intArrA.size) {
        resultArr[indexC++] = intArrA[indexA++]
    }
    while (indexB < intArrB.size) {
        resultArr[indexC++] = intArrB[indexB++]
    }

    return resultArr
}