前言

本文汇总了数据结构的优缺点及应用场景。

通用数据结构：数组、链表、树、哈希表

专用数据结构：栈、队列、优先级队列

排序：冒泡排序、选择排序、插入排序，希尔排序、快速排序、归并排序、堆排序

图：邻接矩阵、邻接表

通用数据结构

这些数据结构使用关键字的值存储、查找数据

其速度如下：

哈希表 > 树 > 链表 > 数组

数组：数据量小，大小可以预测时使用

链表：数据大小不可预知，或需要频繁插入删除元素时使用

前言

本文介绍了二叉树，及其应用。

树，既能像链表那样快速插入和删除，又可以像数组那样快速查找。

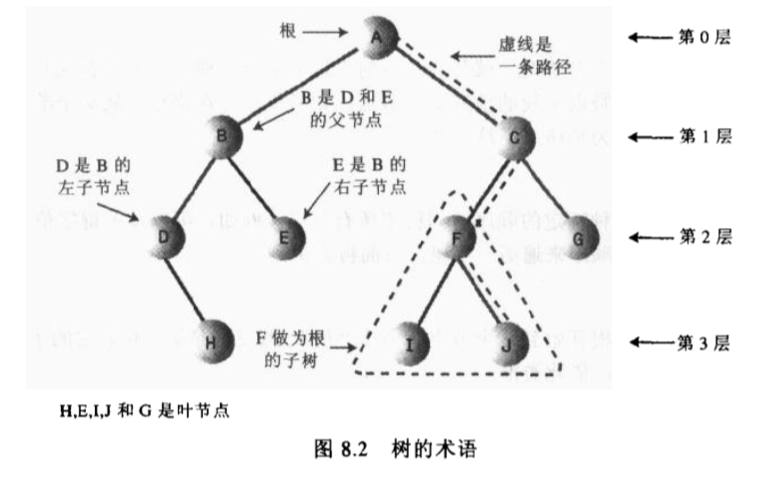
每棵树有且只有一个根，从根到任何一个节点有且只有一条路径；每个节点都可以有 0 个或者多个子节点，没有子节点的节点叫做叶子节点。

前言

本文介绍两种高级排序：希尔排序和快速排序。

希尔排序的时间复杂度是$O(N*(LogN)^2)$，简单易实现，在所有排序中可以优先使用。

前言

本文介绍了递归，归并排序，还有递归在汉诺塔问题上的应用。

排序顺序为 小 → 大

递归

递归是一种在函数内部调用自己的函数。在满足一定条件后可以退出递归。

比如三角数组就是一个简单的递归：

有一组数据，满足这样的条件第n项 = 第n-1项 + n，就称为三角数组，如：

1,2,6,10,15,21...

前言

本文介绍栈、队列两种抽象数据类型。

栈

栈stack，又称堆栈，是一种抽象数据类型，每次只能访问栈顶元素top，可以进行压入push和推出pop操作。其元素先进后出 (FILO)。

队列

队列queue,是和栈相对的一种抽象数据类型，每次从后端rear插入，从前端front删除。其元素先进先出 (FIFO)。

前言

本文介绍了数组、链表等数据结构。

设定所有排序：小 → 大。

数组

数组（array）是一组具有相同类型元素的集合，用一段连续的内存来保存。使用下标来访问保存的元素，如a[0]。

数组是一种数据存储结构。

int a[] = new int[10];

简单排序

所有排序顺序为 小 → 大。

时间负责度都是 O(N²)。

排序速度：插入排序>选择排序>冒泡排序

冒泡排序

时间复杂度：O(N²)

最慢的排序，但是简单

规则如下：

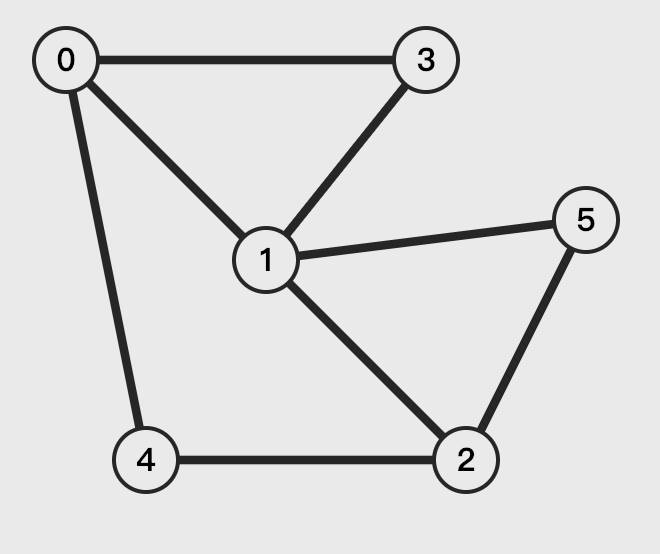
1. 从左到右，比较 a 和 b，如果a>b，就交换 a 和 b 的位置
2. 再将 a，b 中较大的那个与 c 按照 2 的规则比较，直到最后一位
3. 重复 1，2 直到没有待排序的项目

前言

图，是由可以有多个边的顶点组成的结构。

两个顶点之间有边连接，则称这两个顶点是邻接的。

几个相互邻接的顶点组成的线叫做路径,至少有一条路径可以到达所有顶点的图叫做连通图。

如果图的顶点只能从 A→B，不能从 B→A，就称图是有向图。

如果边被赋予一定的权值（数字），就称图为带权图

前言

堆是一种特殊的二叉树，用他实现的优先级队列插入和删除时间复杂度都是$O(LogN)$ 。

前言

Hash 表是一种可以快速插入和查找的数据结构，将数据保存在通过 hash 函数计算得到的下标中。

插入和删除 所需时间为 O(1)。在确定容量、无需遍历时效果最好。

当其大小接近容量时，效率会变得很差。

存储方式

Hash 表有两种存储方式

1. 开放地址法

   开放地址法，直接将数据存储在数组中。

   当 hash 算出的地址已经被占用时，则走过一定的步长找到另外一个空位（在填充质数很大时就会很耗时）并保存数据。

2. 链地址法

   链地址法，创建保存数据的数组，该数组中不直接保存数据，而是保存一个用来存储这些数据的链表，将数据项直接存储的链表中。

   当 hash 算法计算出的地址时，遍历数组中对应的链表找到空位并保存。